关系型数据库设计:模式规范化
7.1 Good Relational DB Design
逻辑数据库设计包括:
- 初始关系架构生成
- 关系架构规范化
Lossless Decomposition无损分解
Def:设 R 为关系模式,R1 和 R2 构成 R 的分解。 即 R = R1 U R2
Def:分解是无损分解,如果将模式 R 替换为两个关系模式 R1 U R2 没有丢失信息
Normalization Principles归一化原则
在DBS逻辑设计过程中,将E-R图转换,得到面向应用领域的初始关系模式集
初始关系模式集存在关系模式属性间的数据依赖 (Data Dependence) 关系
- 函数依赖 (functional dependencies, FD)
- 多值依赖 (Mutivalued Dependencies, MVD)
- 连接依赖 (Join Dependencies, JD)
直接根据初始关系模式构造DBS,由于初始关系模式中数据依赖关系的存在, 可能会违反DB的完整性约束,导致DBS使用的正确性、性能、效率受到影响
- 数据冗余问题 pitfalls
- 插入问题 pitfalls
- 更新问题 pitfalls
- 删除问题 pitfalls
等价变换/模式分解: 对初始关系模式集,保证关系模式的:
- 函数无损连接性(lossless join),
- 函数依赖保持性 (dependency preservation)
关系模式集需要规范化处理——等价变换/模式分解
关系模式规范化主要步骤为:
- 根据函数依赖的Armstrong’s 公理系统和多值依赖的公理系统,从初始关系模式集中已知的函数依赖和多值依赖出发,推导出初始关系模式集中所有的函数依赖和多值依赖
- 对具有函数依赖和多值依赖的初始关系模式集,采用模式分解算法,对其进行(等价)分解和变换,将其转换为各种范式形式,包括:1NF、 2NF、 BCNF、 3NF、 4NF、5NF,以消除函数依赖和多值依赖的负面影响, 保证数据库完整性
第一范式、第二范式、第三范式 - 知乎
关系模式规范化处理的基本要求为:
- 静态关系具有第一范式形式
- 动态关系最好具有3NF或BCNF形式
3种数据依赖间的关系 :
- 函数依赖是特殊的多值依赖
- 多值依赖又是连接依赖的特例
范式1NF、2NF、3NF、BCNF可以看作由符合范式要求的各种关系模式组成的关系模式的集合
e.g. 1NF = { R | R 满足第一范式的定义}
范式间的关系: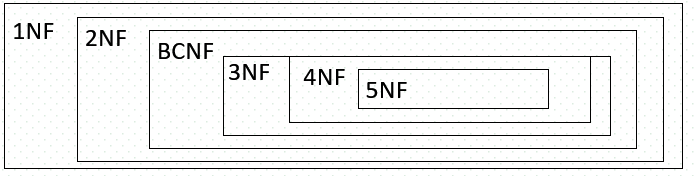

给定关系模式,可以采用规范化算法将其转换为1NF、2NF、3NF、BCNF
对连接依赖和第五范式,无相应的模式规范化算法
Normalization Theory归一化理论
确定特定关系 R 是否处于良好形式(范式)
关系 R 的形式不好,分解为关系 {R1 R2 …Rn} 使得
- 每个关系都处于良好状态
- 分解是无损连接分解
Functional Dependencies功能依赖关系
数据通常存在(完整性)约束(规则)
例如,预期成立的约束:
学生和教师通过其 ID 进行唯一标识。
每个学生和教师只有一个名字。
每个教师和学生只与一个部门相关联。
每个部门只有一个预算值,并且只有一个关联的建筑物
Def:满足所有此类现实世界约束的关系实例称为关系的合法实例
Def:功能依赖:
对法律关系的约束询问
一组特定属性的值唯一地决定了另一组属性的值
函数依赖关系是键概念的泛化
函数: f: X→Y, x∈X, y∈Y, y = f(x)
对于 x1,x2∈X,如果 x1=x2,则 f(x1)= f(x2)
Relation Instance Satisfy Functional Dependency
对于关系模式R,$\alpha$⊆ R,$\beta$⊆ R,满足函数依赖关系$\alpha$→$\beta$
对于元组 ti 和 tj ∈r(R) 对,使得 $t_i[\alpha]= t_j [\alpha ]$,也是 $t_i[\beta]= t_j [\beta]$ 的情况
Functional Dependency Holds on Schema r(R)功能依赖关系保留在架构 r(R) 上
Def:让 R 成为关系架构 $\alpha \subseteq R$ and $\beta \subseteq R$,如果每个实例 r(R) 都满足$\alpha$→$\beta$,函数依赖FD在关系模式R上成立/保持$\alpha$→$\beta$,每当两个元组 t1 和 t2 在属性$\alpha$上达成一致时,也就在$\beta$属性达成一致
FD holds on R vs FD is satisfied by r(R)FD 保持 R 与 FD 满足 r(R)
在 R 上定义可能有多个关系实例 r(R),即$r_1(R) , r_2(R) , r_3(R) ,…, r_m(R)$
定义:关系 r(R) 满足$\alpha$→$\beta$与$\alpha$→$\beta$保留架构 R
如果$\alpha$→$\beta$在 R 上成立,则每个合法 r(R) 都满足此 R
但是对于模式 R,如果只有一些 ri(R) 满足 R,则$\alpha$→$\beta$可能不会对 R 成立。
FD holds on R:
定义在R的属性间的语义约束,或R的属性间体现出的语义约束
从设计角度,R应满足的约束
FD is satisfied by r(R):
根据 R构造的实际数据 r(R) 是否满足语义约束FD
Keys and Functional Dependencies
Def:K 是关系架构 R 的超键,当且仅当 K → R
定义:K 是 R 的候选键,当且仅当 K → R 且 没有 $\alpha \subset$K、$\alpha$→R
DF 允许我们表达无法用超级键表达的约束。
Use of Functional Dependencies
我们使用 FD 来 测试关系,看看它们是否合法。 如果关系 r 在 FD 集合 F 下是合法的,我们说 r 满足 F
指定对法律关系集的约束 如果 R 上的所有法律关系都满足 FD 集 F,则 F 对 R 成立。
注意:关系模式的特定实例可能满足 F 中的 FD,即使 FD 不持有所有法律实例
Trivial (平凡) Functional Dependencies
如果一个关系的所有实例都满足函数依赖关系,那么它就是平凡的
Transitive (传递) dependency
$\alpha$→$\beta$但不满足$\beta$→$\alpha$,满足$\beta$→$\gamma$, 但$\gamma$ 不在$\alpha$内,则称$\alpha$→$\gamma$满足传递依赖关系
Partial (部分) Dependency
y是a的子集,y→b,a→b为部份依赖
Closure of functional dependency set $F^+$
给定 FD 集 F 可以推断的所有 FD 的集合
$F^+$包含 F 中的所有功能依赖项
Lossless Decomposition无损分解
如果至少有如下一个依赖项位于 F+ 中,则将 R 分解为 R1 和 R2 是无损的:
R1 $\cap$R2 →R1
R1$\cap$ R2→ R2
7.3 Normal Forms

1NF:第一范式
2NF:第二范式
BCNF:Boyce-Codd 范式
3NF:第三范式
Atomic Domains and First Normal Form原子域和第一范式
如果域的元素是不可分割的单元,则域是原子的
如果 R 的所有属性的域都是原子的,则关系架构 R 采用第一范式
原子性实际上是如何使用域元素的一个属性
Second Normal Form
关系模式 R 相对于 DF 集 F 在 2NF 中,如果
R 在 1NF 中,并且
每个属性 A 都满足其中一个条件:
- 它出现在候选键中,即它是一个素数属性 // A 是主属性
- 它(不是部分)依赖于候选密钥 A是非主属性,完全依赖于候选键
Boyce-Codd Normal Form, BCNF
Def:关系架构 R 在 BCNF 中相对于 FD 集 F
如果对于 F+ 形式的所有功能依赖关系a→b,a、b属于R,且a→b是传递关系或a是超键
Decomposing a Schema into BCNF将架构分解为 BCNF
设 R 为不在 BCNF 中的架构 R。 让$\alpha$→$\beta$违反 BCNF
我们将 R 分解为
Dependency Preservation依赖关系保留
对于架构 R,F 是在 R 上的功能依赖,并分解 R 的 {R1, R2,.., Rn},F 对 Ri 的限制,表示为 Fi,定义为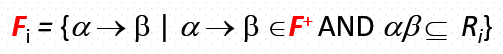
如果满足
则分解是依赖保留关系
由于限制中的所有 FD 都只涉及一个关系模式的属性,因此我们通过仅检查一个关系来测试这种依赖关系。
注意:限制的定义使用 F+ 中的所有依赖项,而不仅仅是 F 中的依赖项。
注意:限制集 F1、F2 、..,Fn 是可以有效检查的 FD 集合。
7.5 Algorithms for Decomposition Using FD
- Testing for BCNF
- Testing Decomposition for BCNF
- BCNF decomposition algorithm
- Testing for 3NF
- 3NF decomposition algorithm
- Comparison of BCNF and 3NF
简化测试:要检查关系架构 R 是否在 BCNF 中,只需检查 F 中的 FD 是否违反 BCNF 就足够了,而不是检查 F+ 中的所有 FD。 如果 F 中没有任何依赖项导致违反 BCNF,则 F+ 中的任何依赖项都不会导致违反 BCNF