前馈神经网络
激活函数
激活函数：最关键部分
- 激活函数：连续并可导的非线性函数
- 激活函数及其导函数要尽可能简单
- 激活函数的导函数要在一个合适的区间内
Sigmoid型函数：指一类S型曲线函数，为两端饱和函数，包括Logistic函数和Tanh函数
- Logistic函数：Logistic 函数可以看成是一个“挤压”函数，把一个实数域的输入“挤压”到 (0, 1)
- Tanh函数：Tanh函数可以看作放大并平移的Logistic函数，其值域是(−1, 1)
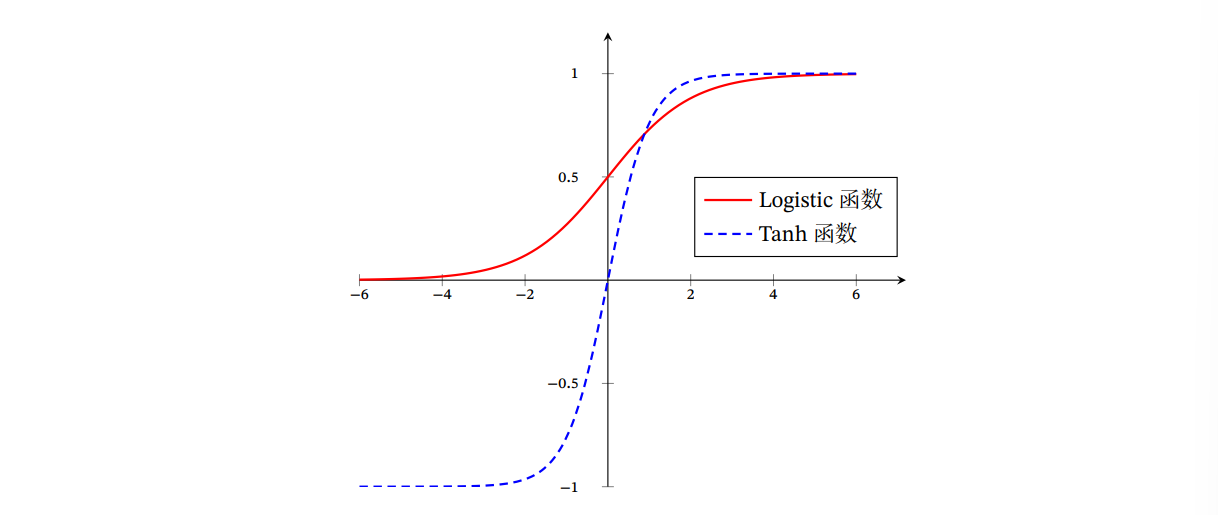
Tanh 函数的输出是零中心化的（Zero-Centered），而 Logistic 函数的输出恒大于 0．非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下 降的收敛速度变慢． - Hard-Logistic函数和Hard-Tanh函数：分段函数来近似Logistic和Tanh
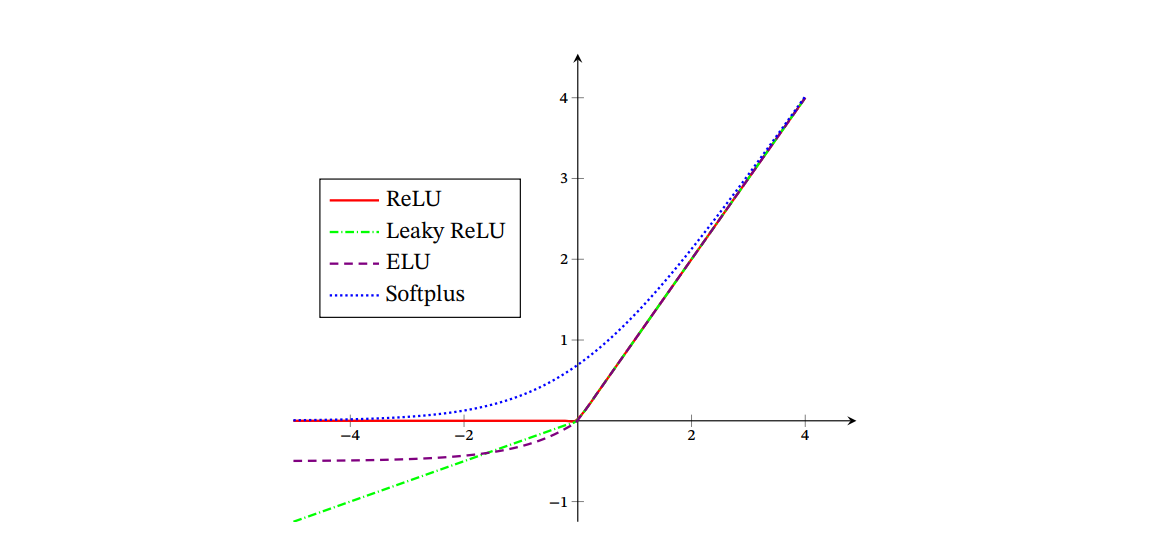
ReLU函数：ReLU（Rectified Linear Unit，修正线性单元）
ReLU为左饱和函数，在 𝑥 > 0 时导数为 1，在一定程度上缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度。ReLU 函数的输出是非零中心化的，给后一层的神经网络引入偏置偏移， 会影响梯度下降的效率。
死亡 ReLU 问题：ReLU 神经元在训练时比较容易“死亡”．在训练时，如果参数在一次不恰当更新后，第一个隐藏层中的某个 ReLU 神经元在 所有的训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是 0，在以后的训练过程中永远不能被激活。
为避免ReLU的问题，有几种ReLU的变种
- 带泄露的ReLU（Leaky ReLU）：在输入 𝑥 < 0时，保持一个很小的梯度𝛾．这样当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不能被激活
- 带参数的ReLU（Parametric ReLU，PReLU）：引入一个可学习的参数
- ELU（Exponential Linear Unit，指数线性单元）
- Softplus 函数
网络结构
- 前馈网络：整个网络中的信息是朝一个方向传播，没有反向的信息传播。包括全连接前馈网络、卷积神经网络等。
- 反馈网络（记忆网络）：和前馈网络相比，记忆网络中的神经元具有记忆功能，在不同的时刻具有不同的状态．记忆神经网络中的信息传播可以是单向或双向传递。
- 图网络：图网络是定义在图结构数据上的神经网络，图中每个节点都由 一个或一组神经元构成．节点之间的连接可以是有向的，也可以是无向的．每个 节点可以收到来自相邻节点或自身的信息
前馈神经网络
每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层．第0层称为输入层，最后一层称0为输出层，其他中间层称为隐藏层．整个网络中无反馈，信号从输入层向输出层单向传播。
传播公式：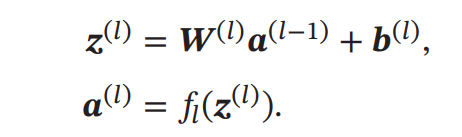
通用近似定理：
根据通用近似定理，前馈神经网络可以以任意精度拟合任意定义在实数空间的有界闭集函数
输出层： 根据任务确定输出层的激活函数
- 回归任务：根据输出的值域选择激活函数
- 分类任务：softmax函数
反向传播算法
假设采用随机梯度下降进行神经网络参数学习，给定一个样本 (𝒙, 𝒚)，将其 输入到神经网络模型中，得到网络输出为 𝒚̂．假设损失函数为 ℒ(𝒚, 𝒚)̂，要进行参数学习就需要计算损失函数关于每个参数的导数。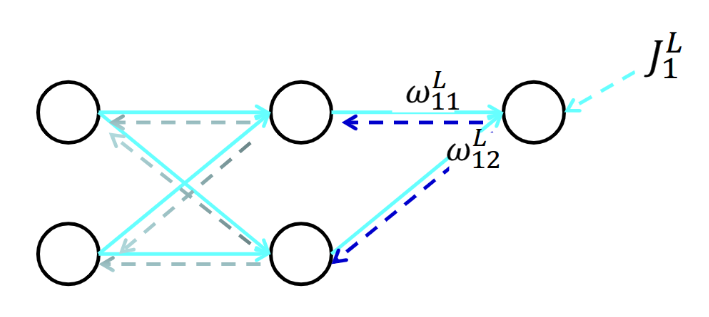
根据损失函数计算参数的偏导数：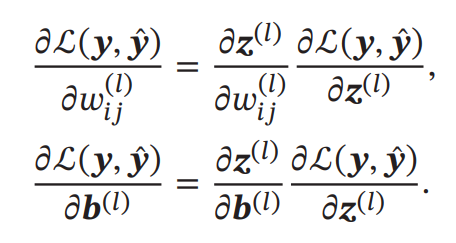
偏导数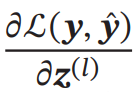
表示第𝑙层神经元对最终损失的影响，也反映了最终损失对第𝑙 层神经元的敏感程度，因此一般称为第𝑙 层神经元的误差项，用𝛿 (𝑙) 来表示．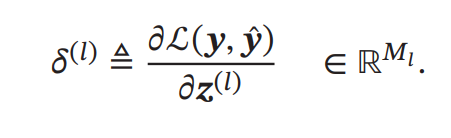
误差项𝛿 (𝑙) 也间接反映了不同神经元对网络能力的贡献程度
第𝑙 层的误差项可以通过第𝑙 + 1层的误差项计算得到，这就是误差的反向传播（BackPropagation，BP）。反向传播算法的含义是： 第 𝑙 层的一个神经元的误差项（或敏感性）是所有与该神经元相连的第 𝑙 + 1 层 的神经元的误差项的权重和．然后，再乘上该神经元激活函数的梯度。
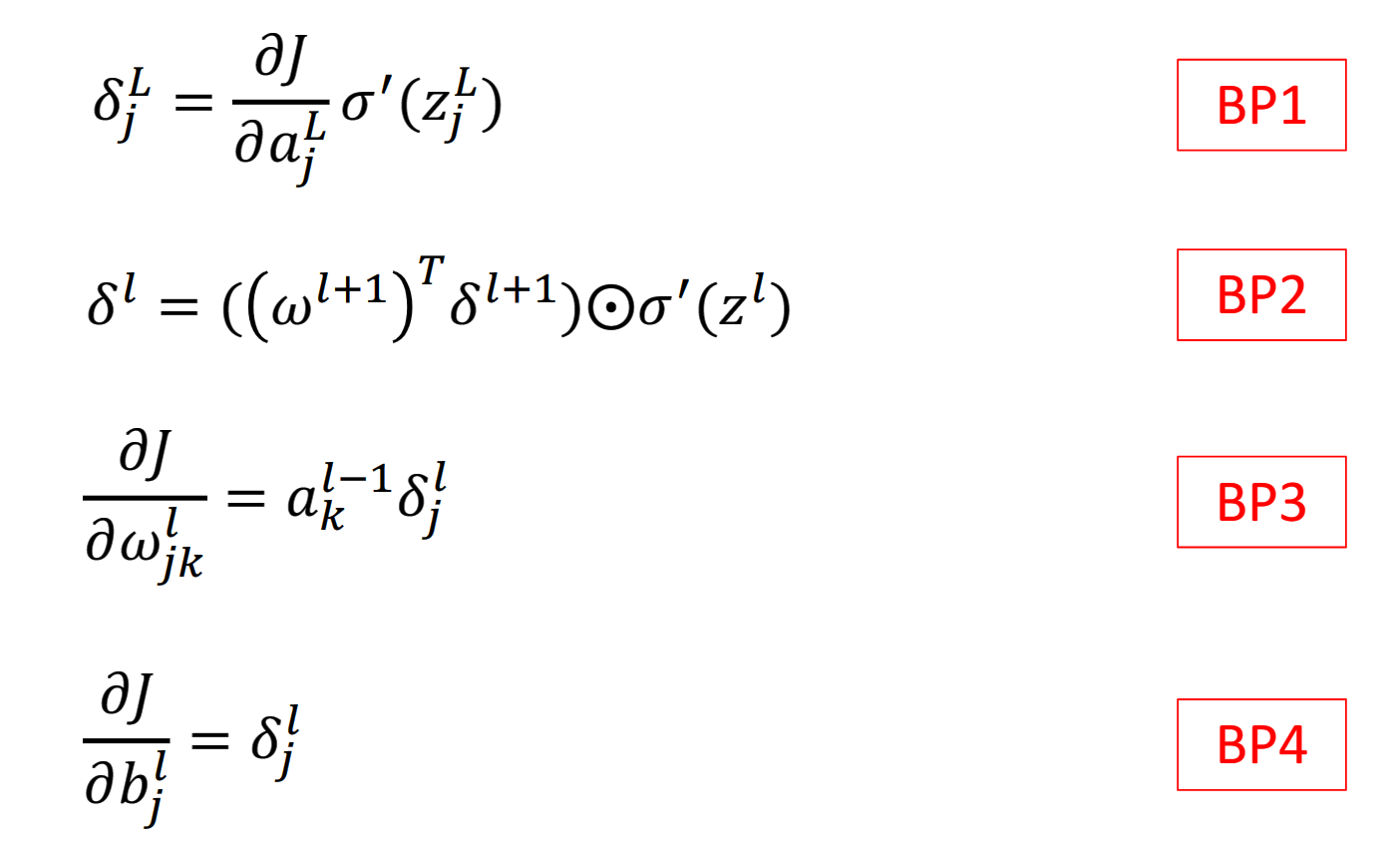
需要会推导
优化问题
神经网络的参数学习比线性模型要更加困难，主要原因有两点：1）非凸优化问题和2）梯度消失问题．
非凸优化问题
凸优化问题:
对于目标函数，我们限定是凸函数；对于优化变量的可行域（注意，还要包括目标函数定义域的约束），我们限定它是凸集。同时满足这两个限制条件的最优化问题称为凸优化问题，这类问题有一个非常好性质，那就是局部最优解一定是全局最优解。
神经网络的优化问题是一个非凸优化问题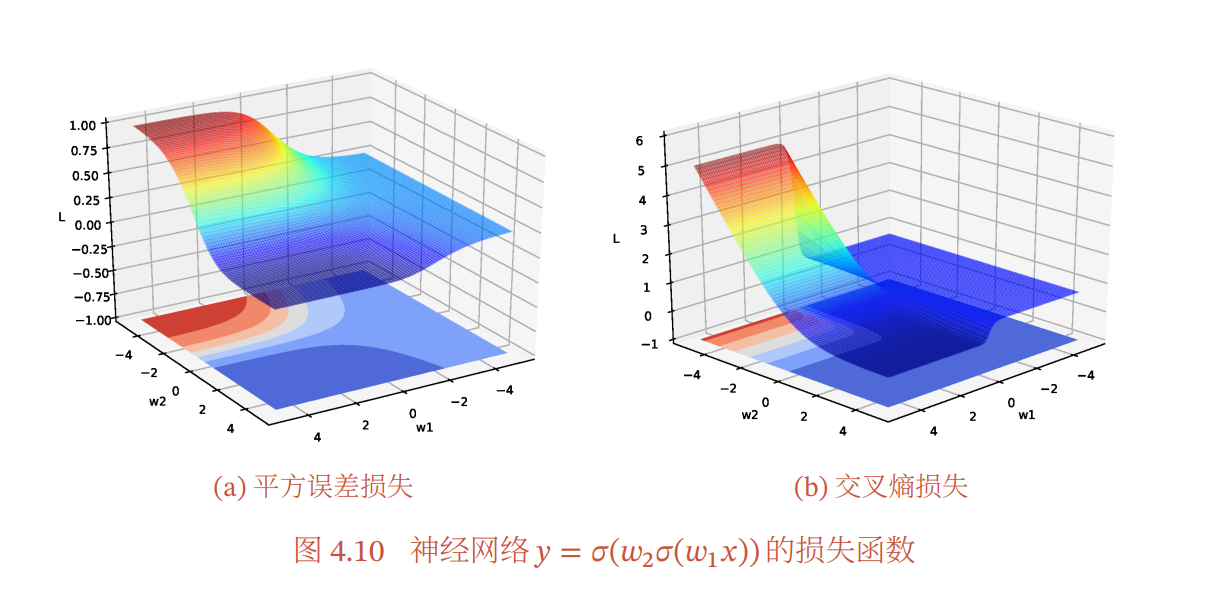
梯度消失问题
误差从输出层反向传播时，在每一层都要乘以该层的激活函数的导数．当我们使 用Sigmoid型函数：Logistic函数𝜎(𝑥)或Tanh函数时，其导数为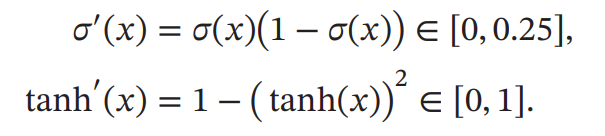
其导数的值域都小于等于1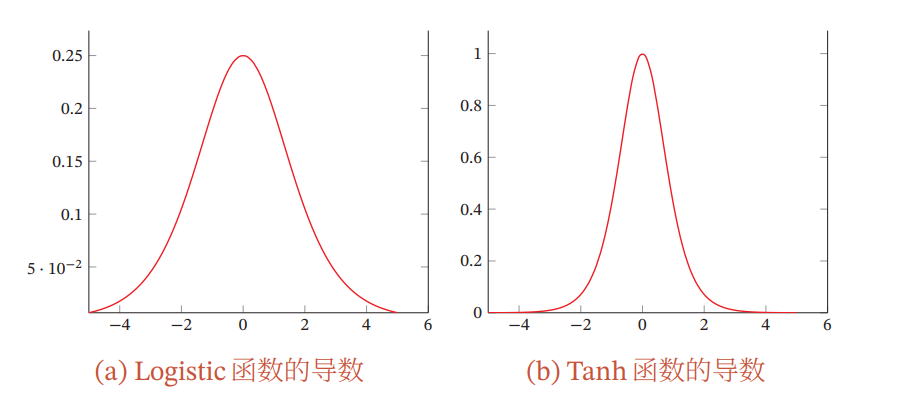
由于 Sigmoid 型函数的饱和性，饱和区的导数更是接近于 0．这样，误差经过每一层传递都会不断衰减．当网络层数很深时，梯度就会不停衰减，甚至消失，使得整个网络很难训练．这就是所谓的梯度消失问题（Vanishing Gradient Problem）.
在深度神经网络中，减轻梯度消失问题的方法有很多种．一种简单有效的方式是使用导数比较大的激活函数，比如ReLU等。