生成模型
有监督:
给定数据(x,y),x为输出,y是对应的标签
目的:学习一个映射f: x→y
用于分类、回归、目标检测、语义分割、图像描述等
无监督:
数据:只有x,没有标签
目标:学习隐藏的信息(数据背后隐藏的结构、主题、情感等)
用于聚类、特征降维、特征学习、密度估计等
判别模型:
同时需要输入X和标签Y,试图通过某个判别函数建模条件分布P(Y|X)
例如softmax回归,SVM等
不能建模P(X),即观测到某个样本的概率
生成模型:
不需要标签Y,试图建模P(X, Y), P(X|Y), P(X)等
可以建模P(X),可以生成新的样本
显式的密度估计:显式定义和求解$p_{model}(x)$,最大似然估计、马尔科夫链
隐式的密度估计:学习一个可以从中抽样出样本的模型$p_{model}(x)$,但并不显式定义它,GAN
隐变量模型
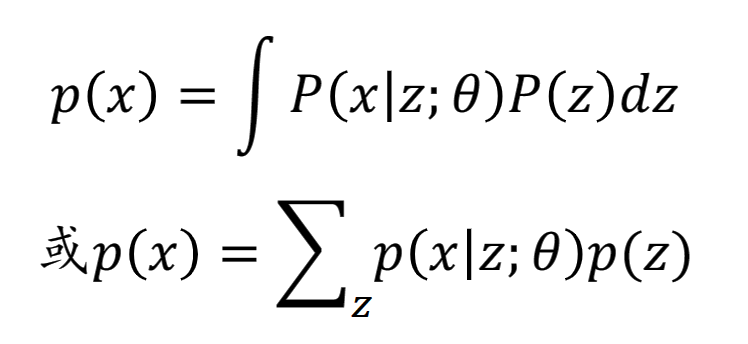
借助因变量z,$p(x|z;\theta)$可以用$f(z,\theta)$逼近,进而把概率密度估计问题转化为函数逼近问题
蒙特卡洛采样法
对大多数任务来说,精确估计往往不可行,因而转为近似估计
蒙特卡洛技术是建立在数值采样基础上的近似推断方法

穷尽所有的z非常困难
缩小z的取值范围:原本从任意分布P(z)中采样得到z→变为从后验分布p(z|X)中采样得到z
变分自动编码器
变分推断是一种通过函数最优化近似估计概率的方法
基本思想:提出一个分布家族,进一步从中得到一个接近目标分布的分布
编码器:采样神经网络学习z的分布p(z),例如高斯分布,从p(z)中抽样一个z
解码器:采用另一个神经网络从p(x|z)抽样得到x
改良:原本从任意分布P(z)中采样得到z→变为从后验分布p(z|X)中采样得到z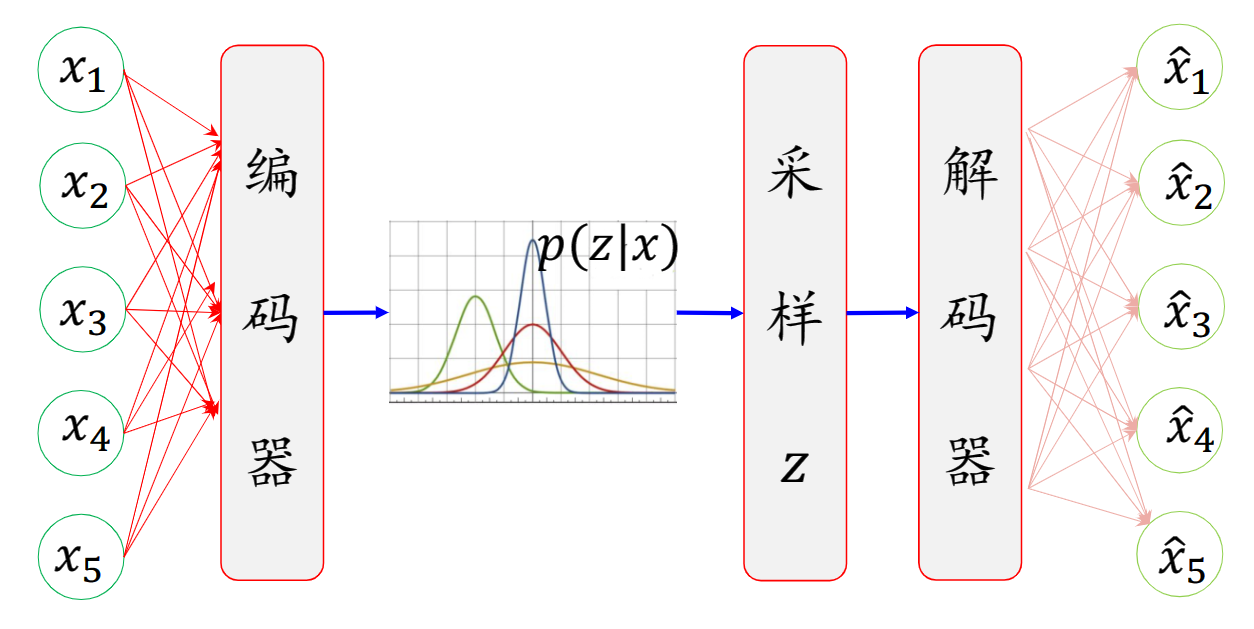
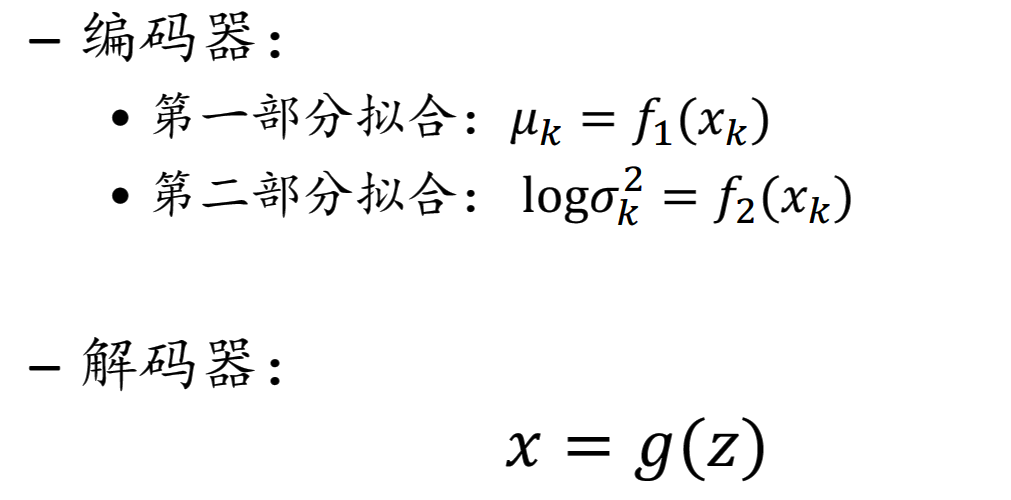
目标函数:学习模型参数$\theta$,以最大化训练数据的对数似然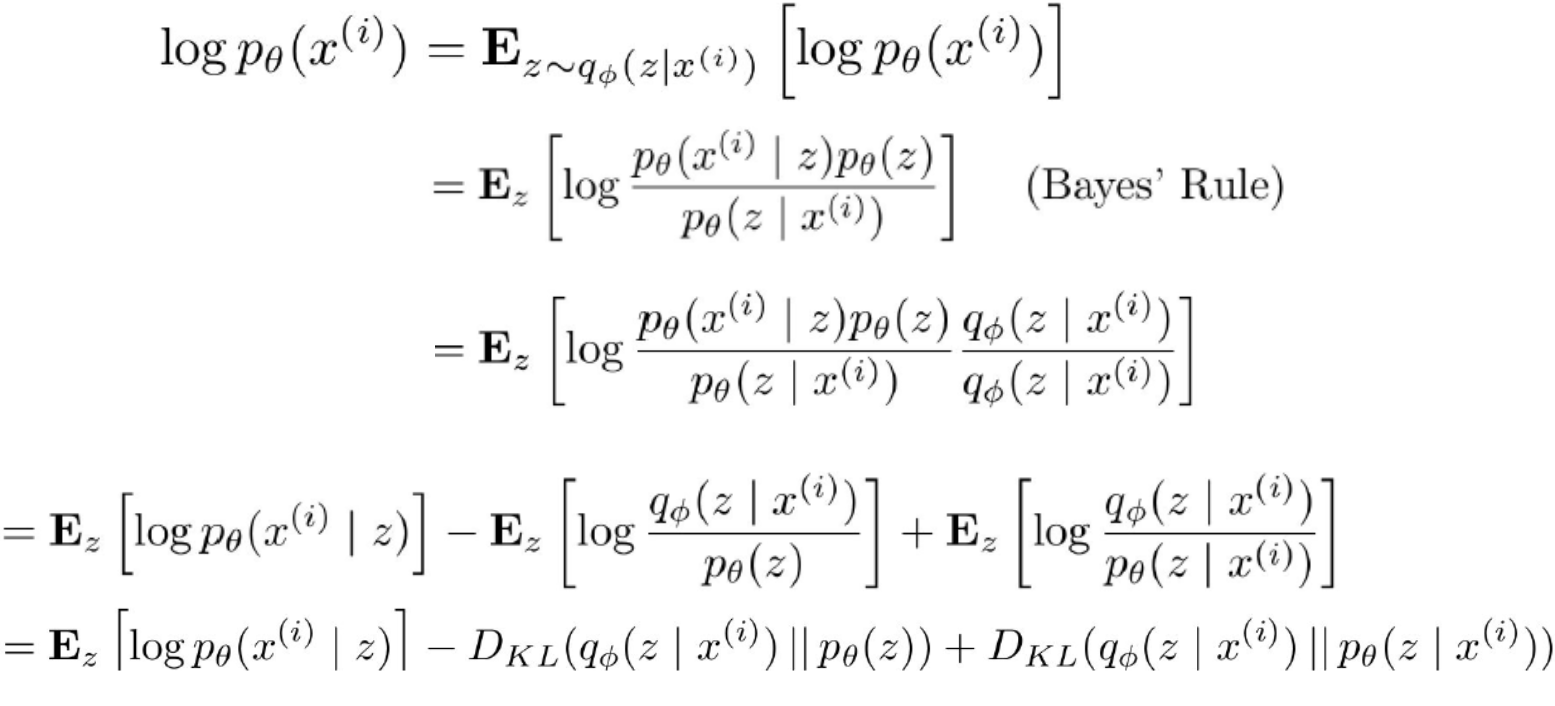
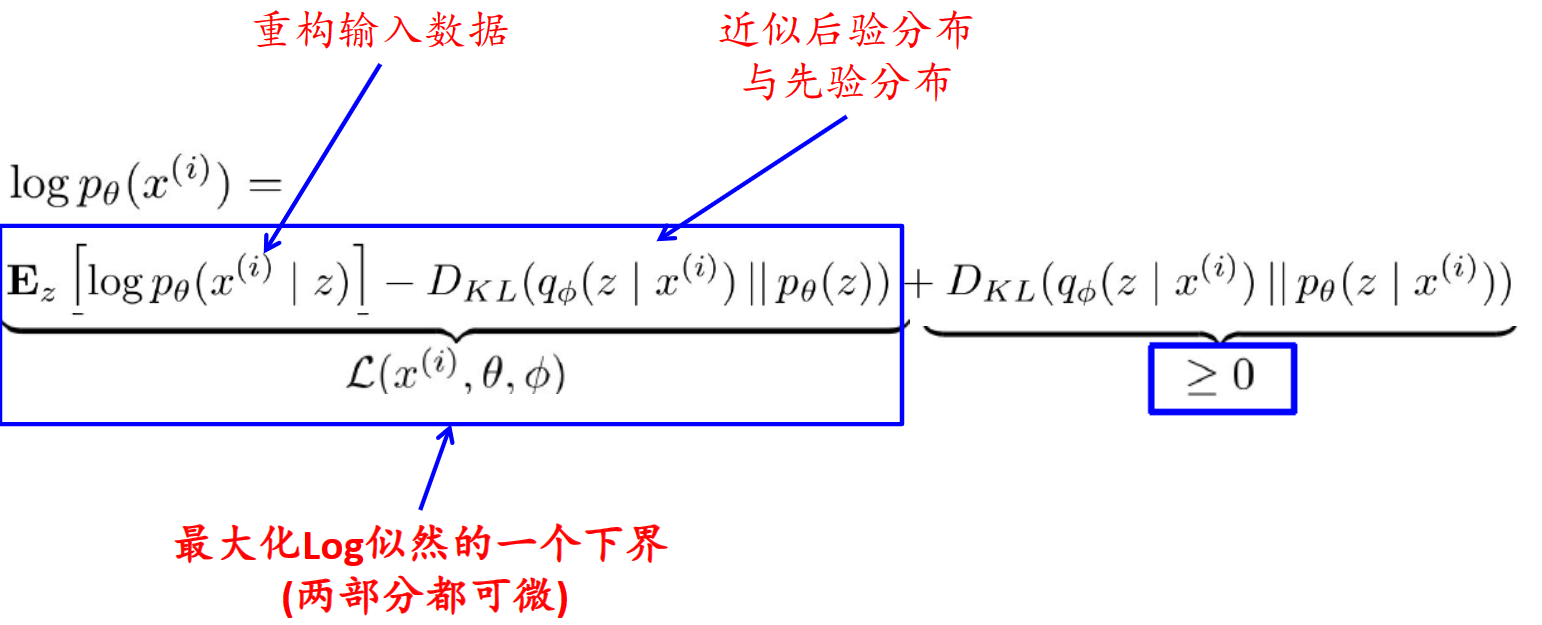
训练:最大化下界(ELBO)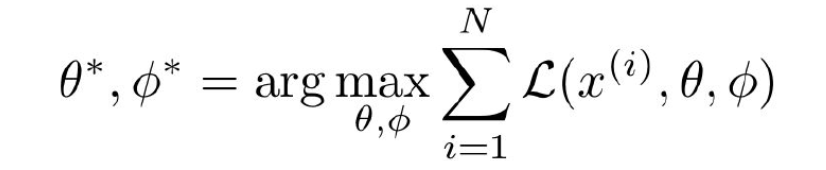

Conditional VAE
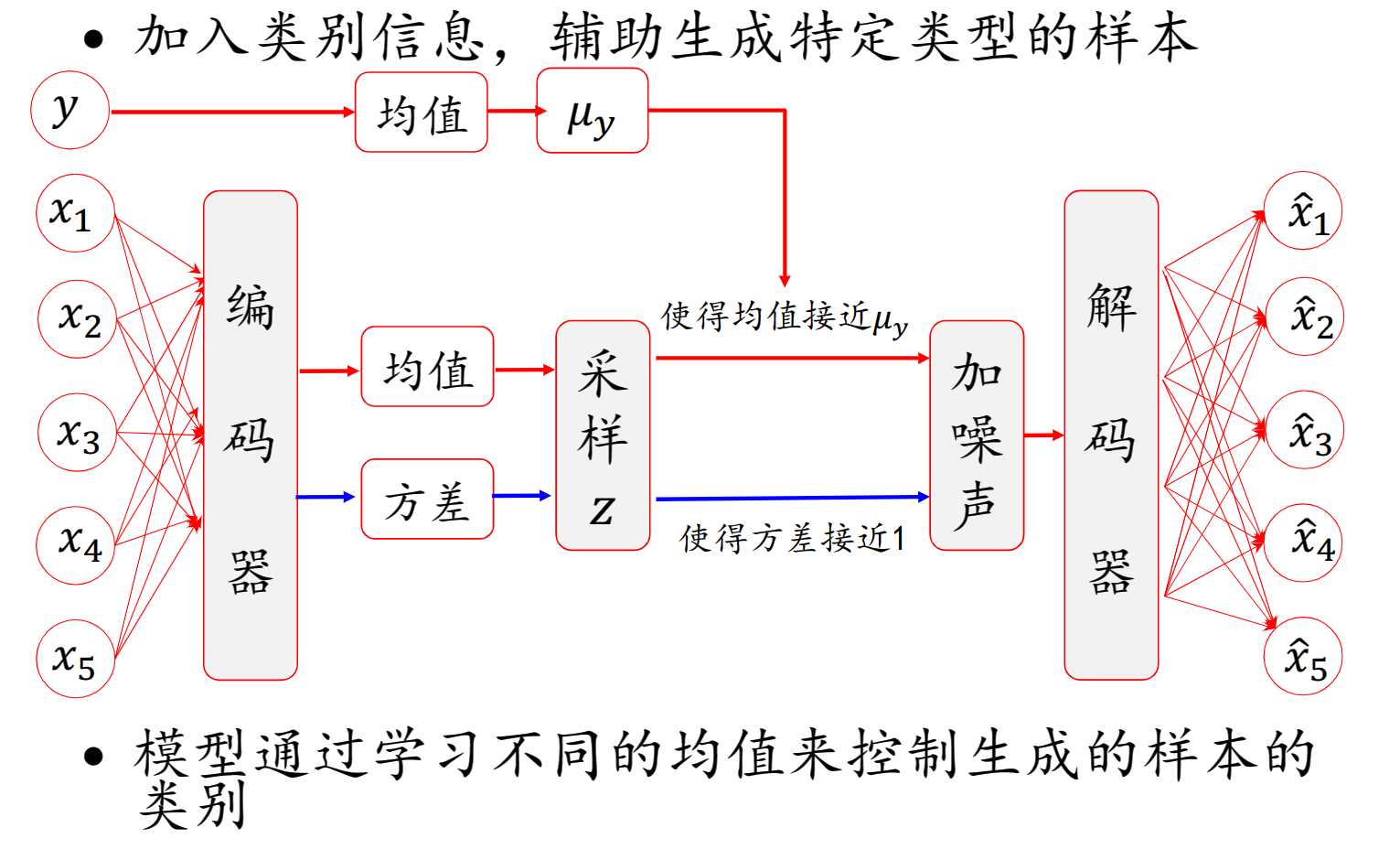
生成模型
http://example.com/2024/11/27/Notes/课程/大三(上)/神经网络与深度学习/生成模型/