A2分析与简答

• A2.1 (5 points) 尝试解释Epoch、Iteration、Batch几个概念及其不同，尝试说明batch_size的选择依据和影响。

Epoch代表全部的训练数据在模型中训练的次数
Iteration表示在一个Epoch中参数更新的次数
Batch表示一次正向和反向传播中的一组数据样本
batch_size表示Batch中的数据量。小的batch_size可能会导致训练过程不稳定，但梯度更新更快，更容易得到更好的模型效果。大的batch_size可以提高内存利用率，训练效果比较稳定，但模型收敛速度较慢，过大的batch_size得到的模型效果普遍较差。

• A2.2 (5 points) 以一个简单的1-1-1结构的两层神经网络为例，分别采用均方误差损失函数和交叉熵损失函数，说明这两种函数关于参数的非凸性（可作图示意和说明）。

该网络表达式为：$$a_{1} = w_{1}\cdot x + b_{1}$$$$a_{2} = w_{1}\cdot a_{1} + b_{2}$$
均方误差损失函数表达式为：$$L\left(y, a_{2}\right)=\left(y-a_{2}\right)^{2}$$画出函数关于 $w_{1}$ 和 $b_{1}$ 的曲面图如下：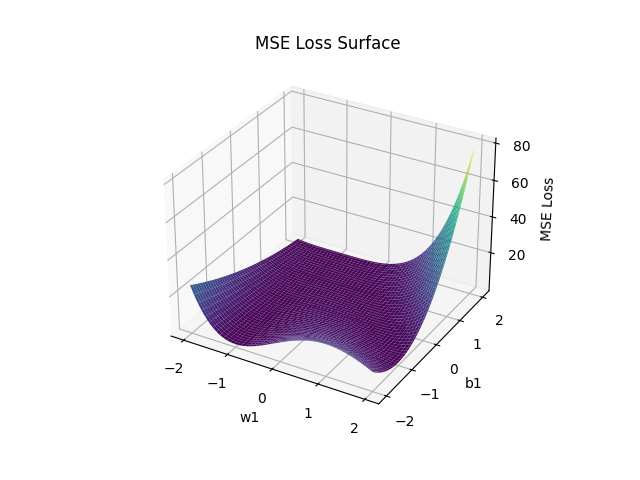

交叉熵损失函数表达式为：$$L\left(y, a_{2}\right)=-\left[y \log \left(a_{2}\right)+(1-y) \log \left(1-a_{2}\right)\right]$$画出函数关于 $w_{1}$ 和 $b_{1}$ 的曲面图如下：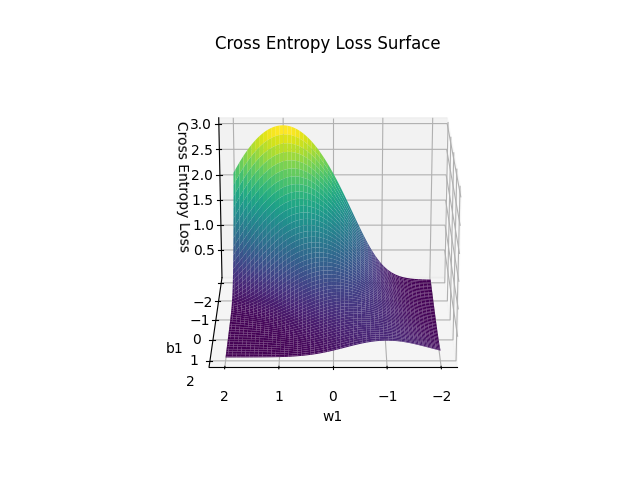
由图像可以显然看出其非凸性

• A2.3 (5 points) 尝试推导：在回归问题中，假设输出中包含高斯噪音，则最小化均方误差等价于极大似然。

回归模型中输出加入高斯噪音，用函数表示如下：$$y=f(x, \theta)+\epsilon$$其中 $x$ 为输入数据，$y$ 为输出数据，$\epsilon$ 为高斯噪音，在此假设其概率密度函数为 $\mathcal{N}\left(0, \sigma^{2}\right)$.
对于一个期望为 $\mu$ ，方差为 $\sigma^{2}$ 的正态分布，其概率密度函数为：$$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)$$
样本 $y_i$ 服从期望为 $f(x_i, \theta)$ ，方差为 $\sigma^{2}$ 的正态分布，其概率密度函数为：$$p\left(y_{i} \mid x_{i}, \theta\right)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{\left(y_{i}-f\left(x_{i}, \theta\right)\right)^{2}}{2 \sigma^{2}}}$$
所有样本的联合概率密度函数为：$$p(\mathbf{y} \mid \mathbf{x}, \theta)=\prod_{i=1}^{N} p\left(y_{i} \mid x_{i}, \theta\right)=\frac{1}{\left(2 \pi \sigma^{2}\right)^{N / 2}} e^{-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{N}\left(y_{i}-f\left(x_{i}, \theta\right)\right)^{2}}$$
极大似然估计的目的是找到使得观测数据出现的概率最大的参数值 $\theta$ ，即调整 $\theta$ 的值使得上述联合概率密度函数的值最大，即使得 $\sum_{i=1}^{N}\left(y_{i}-f\left(x_{i}, \theta\right)\right)^{2}$ 的值最小。

样本的均方误差可以表示为：$$MSELoss=\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-f\left(x_{i}, \theta\right)\right)^{2}$$最小化均方误差即使得 $\sum_{i=1}^{N}\left(y_{i}-f\left(x_{i}, \theta\right)\right)^{2}$ 的值最小，这与极大似然估计的目的等价。

• A2.4 (5 points) 尝试推导：在分类问题中，最小化交叉熵损失等价于极大化似然

极大似然估计与最小化交叉熵损失或者KL散度为什么等价？ - 知乎
分类问题的联合概率分布为：$$p(X \mid \theta) = \prod_{i=1}^{N} p\left(x^{(i)} \mid \theta\right) = \frac{1}{N} \sum_{i=1}^{N} \log p\left(x^{(i)} \mid \theta\right)$$
对参数 $\theta$ 的极大似然估计为：$$\begin{array}{l}
\theta=\underset{\theta}{\operatorname{argmax}} p(X \mid \theta) \
=\underset{\theta}{\operatorname{argmax}} \prod_{i=1}^{N} p\left(x^{(i)} \mid \theta\right) \
=\underset{\theta}{\operatorname{argmax}} \frac{1}{N} \prod_{i=1}^{N} p\left(x^{(i)} \mid \theta\right) \
=\underset{\theta}{\operatorname{argmax}} \frac{1}{N} \sum_{i=1}^{N} \log p\left(x^{(i)} \mid \theta\right)
\end{array}$$抽样服从真实样本分布，可得：$$\begin{array}{l}
=\underset{\theta}{\operatorname{argmax}} E_{x \sim p_{\text {data }}(x)} \log p(x \mid \theta) \
=\underset{\theta}{\operatorname{argmax}} \int_{x} p_{\text {data }}(x) \log p(x \mid \theta) d x \
=\underset{\theta}{\operatorname{argmin}} \int_{x}-p_{\text {data }}(x) \log p(x \mid \theta) d x
\end{array}$$即为交叉熵损失。

• A2.5 (5 points) 分析为什么L1正则化倾向于得到稀疏解、为什么L2正则化倾向于得到平滑的解。

l1 相比于 l2 为什么容易获得稀疏解？ - 知乎
L1正则化项是参数的绝对值之和，它在零附近不可导，这使得在优化过程中，某些参数可能会被推到零，从而使得模型变得稀疏；
L2正则化项是参数的平方和，它是光滑可导的，在优化过程中会使得所有参数都变得较小，但通常不会等于零，从而得到一个相对平滑的解。

• A2.6 (5 points) 分析Batch normalization对参数优化起到什么作用、如何起到这种作用。

允许使用更大的学习率，加快模型的学习速度。减轻了对参数初始化的依赖，一定程度上增加了泛化能力。
Batch normalization对每个batch中的数据进行归一化，使得其均值为0，方差为1，然后进行缩放和偏移操作（scale and shift），维持数据的原始分布，其均值和方差分别为可学习的参数β和γ，通过反向传播更新。